高数基础（二）导数与微分
导数与微分的概念
导数的概念
【注】f’(x_0)与f(x_0)有关
例题1
例题2
微分的概念
例题3
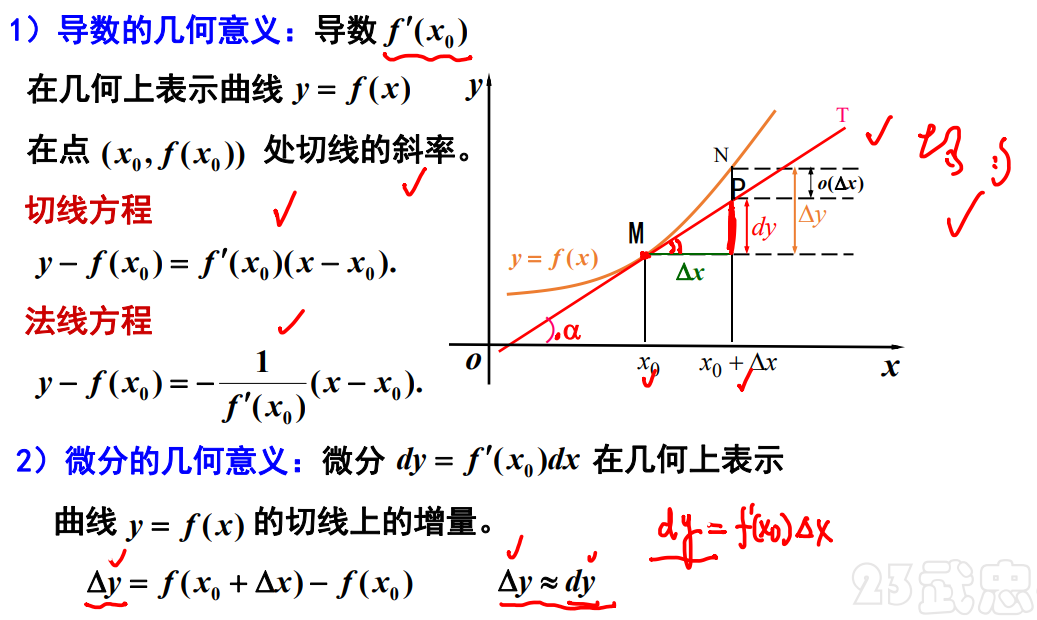
导数与微分的几何意义
例题4
连续、可导、可微之间的关系
【注】n阶可导，用洛必达法则，最多可以用到出现n-1阶可导；n阶连续可导，用洛必达法则，最多可以用到出现n阶可导。如：二阶可导，用洛必达法则，最多可以用到出现一阶可导，不能出现二阶可导
例题5
导数公式及求导法则
基本初等函数的导数公式
求导法则
例题7~8
隐函数求导法
反函数的导数
参数方程求导法
例题11
对数求导法
例题13
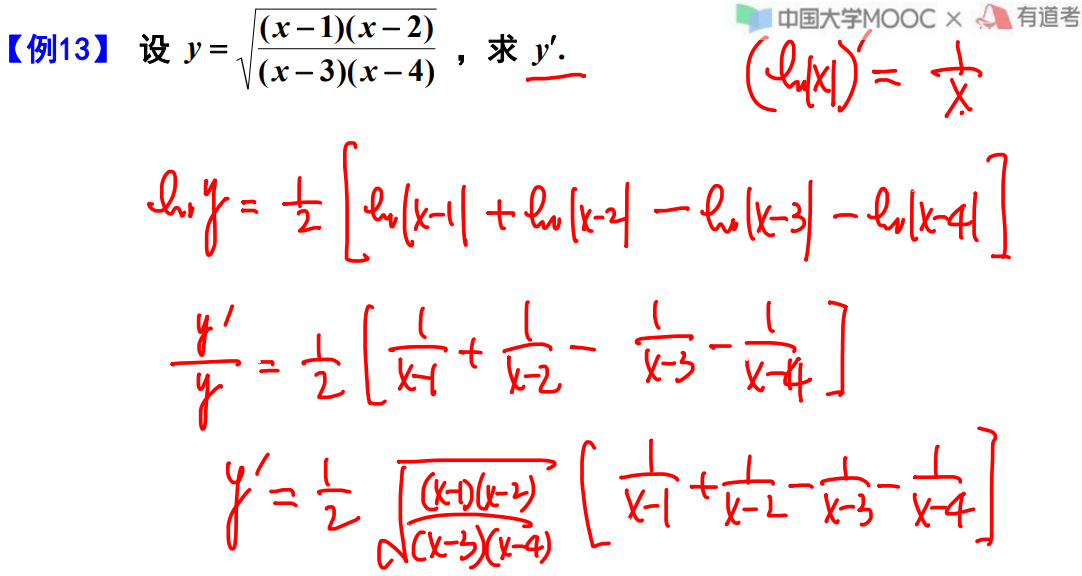
总结
高阶导数
高阶导数的概念
常用的高阶导数公式
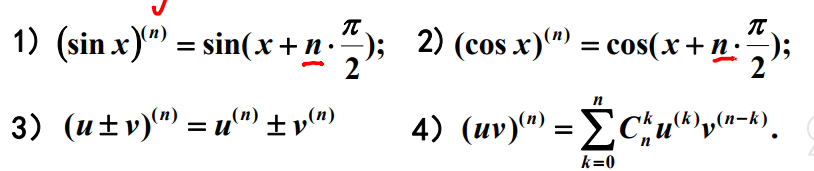
例题14~15
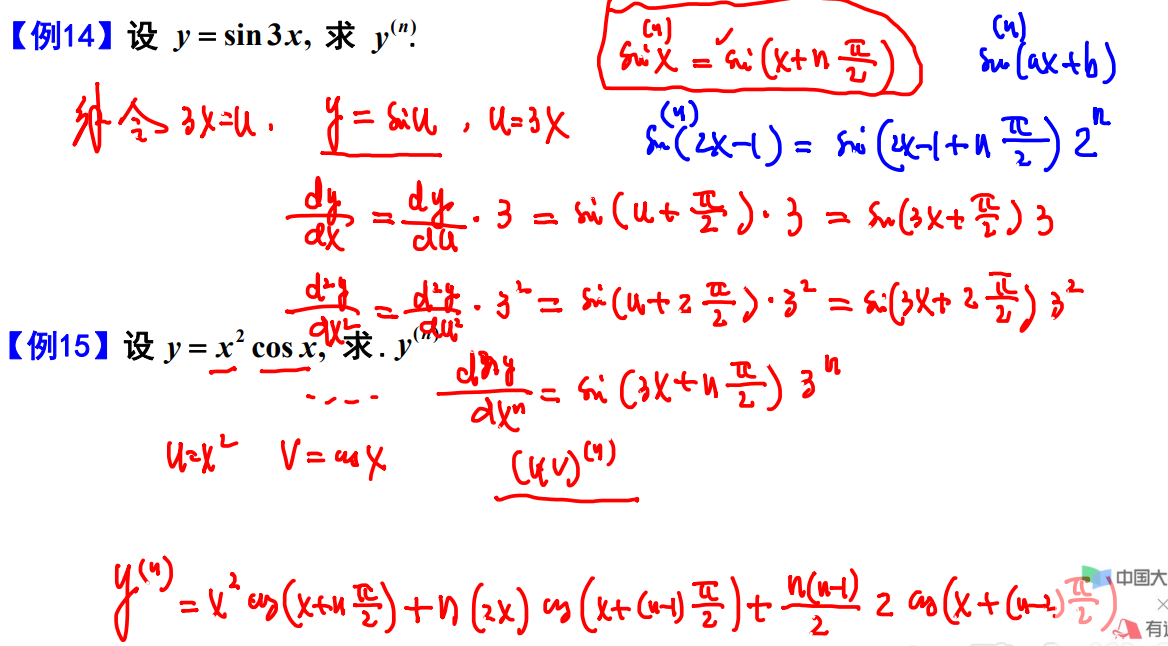
常考题型与典型例题
1、导数定义
2、复合函数、隐函数、参数方程求导
3、高阶导数
4、导数应用
例题16
例题17
例题18
例题19
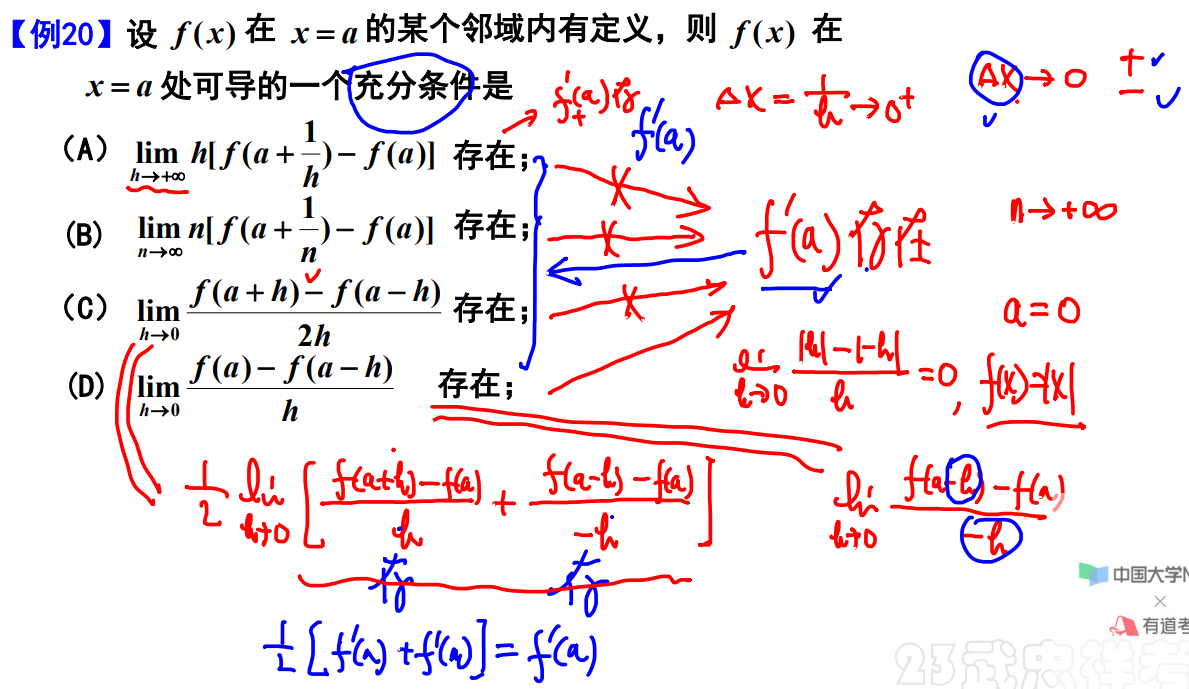
例题20
例题21
例题22
例题23
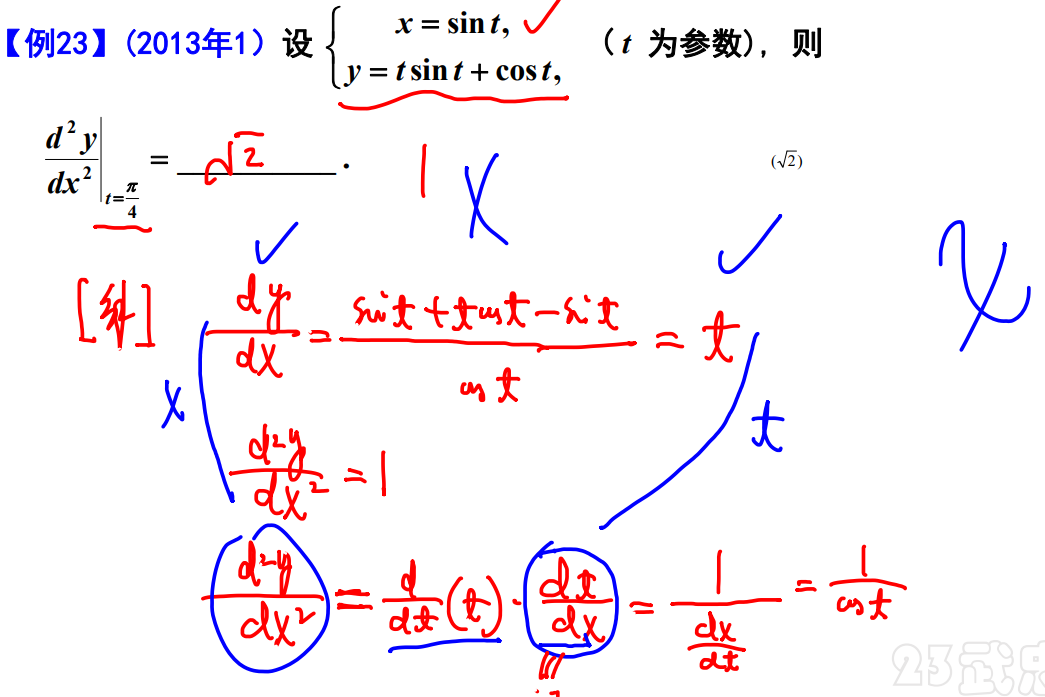
例题24
例题25
例题26
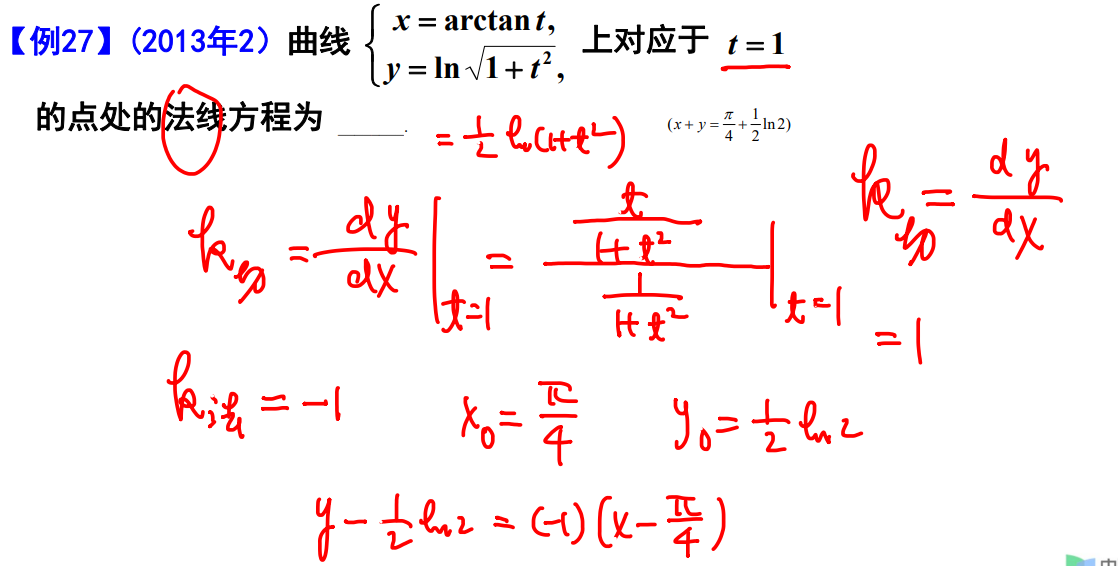
例题27
例题28
例题29
内容取自武忠祥老师基础班教程，参考书《高等数学·基础篇》
本博客所有文章除特别声明外，均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 LUCKY！
微信
支付宝
相关推荐
2023-03-21
高数基础（一）函数 极限 连续
第一节 函数导论 函数的概念及常见函数函数概念 符号函数、取整函数 复合函数 反函数 例题3 初等函数 函数的性质单调性 奇偶性 例题4 周期性 有界性 例题5 第一节常考题型与典型例题1、函数有界性、单调性、周期性及奇偶性的判定（函数的性质） 2、复合函数 例题6 例题7 例题8 第二节 极限极限的概念数列的极限 【注】极限的几何意义：①b＜a（a就是极限A），当存在N，当n＞N时，x_n＞b;②c＞a（a就是极限A），当存在N，当n＞N时，x_n＜c 例题1 例题2 【注】 ||a|-|b||≤|a-b| 函数的极限自变量趋于无穷大时函数的极限 【注】 函数的极限中x一>∞是指|x|一>+∞（x一>-∞/x一>+∞）；而数列极限中的n一>∞是指n一>+∞. 自变量趋于有限值时函数的极限 例题3 例题4 极限的性质有界性 【注】...
2023-04-18
高数基础（七）微分方程
常微分方程的基本概念 一阶微分方程可分离变量的方程 例题1 齐次微分方程 例题2 一阶线性微分方程 例题3 可降阶的高阶方程（数三不要求） 例题4 例题5 高阶线性微分方程线性微分方程的解的机构 常系数齐次线性微分方程 例题6 例题7 例题8 常系数非次线性微分方程 例题9 例题10 常考题型与典型例题1、方程求解 2、综合题 3、应用题 例题16 例题17 例题18 例题19 例题20 例题21 例题22 例题23 例题24 例题25 例题26 例题27 例题28 例题29 例题30 例题31 内容取自武忠祥老师基础班教程，参考书《高等数学·基础篇》
2023-04-12
高数基础（三）微分中值定理及导数应用
微分中值定理 导数应用函数的单调性 函数的极值 函数的最大值与最小值 曲线的凹凸性 【注】：①连续曲线弧上的凹与凸的分界点称为曲线弧的拐点。...
2023-04-18
高数基础（九）二重积分
二重积分的概念及性质二重积分的概念及二重积分的性质 二重积分的计算利用直角坐标系计算 利用极坐标计算 利用函数的对称性和奇偶性计算 利用变量对称性计算 常考题型与典型例题1、累次积分交换次序或计算 2、二重积分计算 例题1 例题2 例题3 例题4 例题5 例题6 例题7 例题8 例题* 例题9 例题10 例题11 例题12 例题* 内容取自武忠祥老师基础班教程，参考书《高等数学·基础篇》
2023-04-18
高数基础（五）定积分与反常积分
第一节 定积分定积分的概念定积分的定义 定积分存在的充分条件及定积分的几何意义 定积分的性质不等式性质及中值定理 积分上限的函数 定积分的计算5种定积分的计算方法 第一节常考题型与典型例题1、定积分的概念、性质及几何意义 2、定积分的计算 3、变上限积分 例题1 例题2 例题3 例题4 例题5 例题6 例题7 例题8 例题9 例题10 例题11 例题12 例题13 例题14 例题15 例题16 例题17 例题18 例题19 例题20 例题21 例题22 例题23 例题24 例题25 例题26 第二节 反常积分无穷区间上的反常积分 例题1 无界函数的反常积分 例题2 第二节常考题型与典型例题1、反常积分的敛散性 2、反常积分的计算 例题3 例题4 例题5 例题6 例题7 例题8 例题9 内容取自武忠祥老师基础班教程，参考书《高等数学·基础篇》
2023-04-18
高数基础（八）多元函数微分学
第一节 多元函数的基本概念多元函数的极限 例题1 例题2 多元函数的连续性连续的概念 连续函数的性质 偏导数偏导数的定义 二元函数偏导数的几何意义 高阶偏导数 全微分 连续、可偏导及可微之间的关系 第一节常考题型与典型例题多元函数连续、偏导数、全微分的概念及其之间的关系 例题3 例题4 例题5 例题6 例题7 第二节 多元函数的微分法复合函数微分法 隐函数微分法 第二节常考题型与典型例题复合函数及隐函数的偏导数和全微分的计算 例题1 例题2 例题3 例题4 例题5 例题6 例题7 例题8 例题9 例题10 例题11 例题12 例题13 第三节 多元函数的极值与最值无约束极值 条件极值极拉格朗日乘数法 最大最小值 第三节常考题型与典型例题1、求极值（无条件） 2、求连续函数ƒ(x,y)在有界闭域D上的最大最小值 3、最大最小值应用题 例题1 例题2 例题3 例题4 例题5 例题6 内容取自武忠祥老师基础班教程，参考书《高等数学·基础篇》
