高数基础(八)多元函数微分学
第一节 多元函数的基本概念
多元函数的极限

例题1

例题2

多元函数的连续性
连续的概念
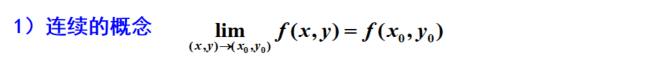
连续函数的性质


偏导数
偏导数的定义
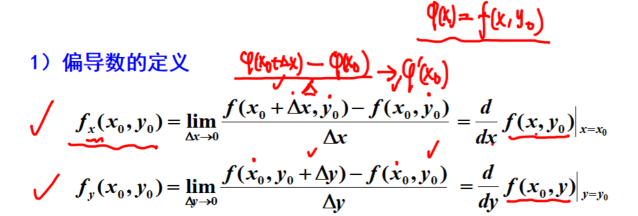
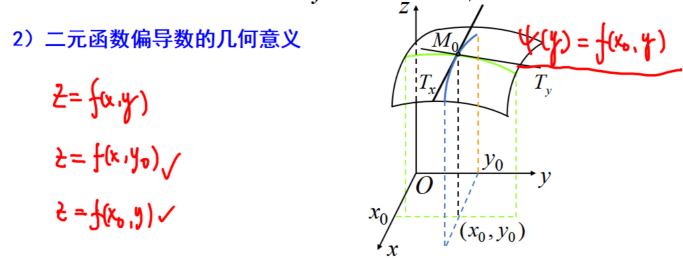
二元函数偏导数的几何意义
高阶偏导数

全微分


连续、可偏导及可微之间的关系
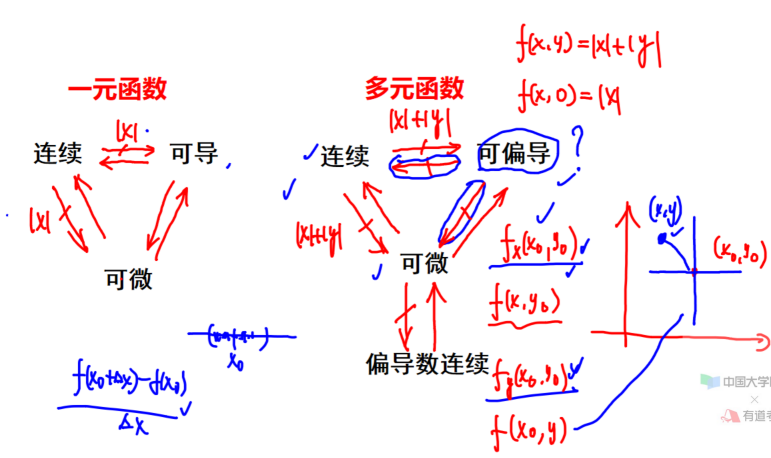
第一节常考题型与典型例题
多元函数连续、偏导数、全微分的概念及其之间的关系
例题3

例题4

例题5

例题6





例题7

第二节 多元函数的微分法
复合函数微分法

隐函数微分法

第二节常考题型与典型例题
复合函数及隐函数的偏导数和全微分的计算
例题1


例题2

例题3
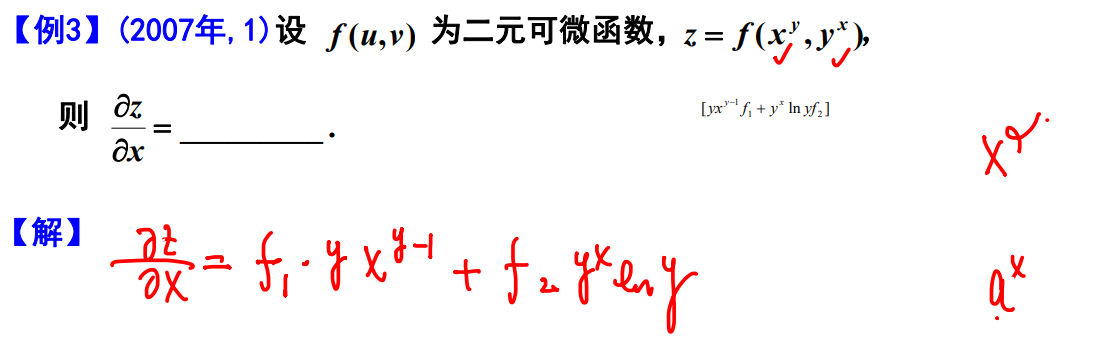
例题4

例题5

例题6

例题7


例题8

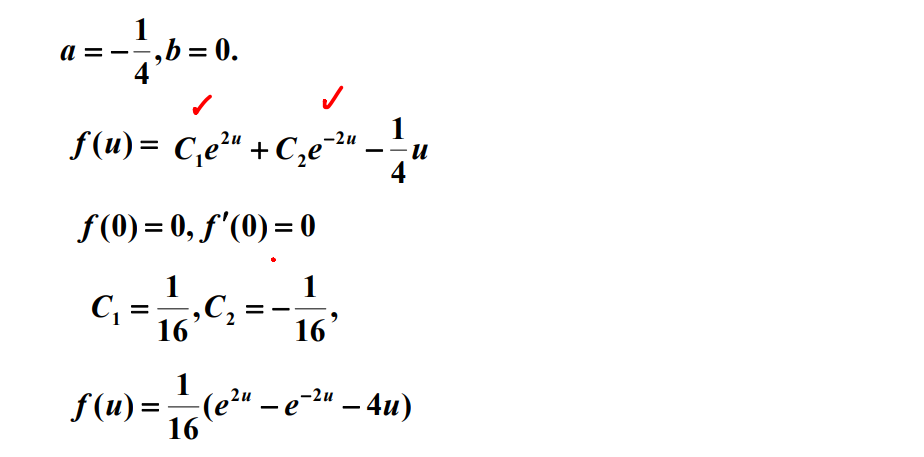
例题9


例题10

例题11

例题12


例题13


第三节 多元函数的极值与最值
无约束极值


条件极值极拉格朗日乘数法

最大最小值

第三节常考题型与典型例题
1、求极值(无条件)
2、求连续函数ƒ(x,y)在有界闭域D上的最大最小值
3、最大最小值应用题
例题1

例题2



例题3

例题4

例题5

例题6



内容取自武忠祥老师基础班教程,参考书《高等数学·基础篇》
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来源 LUCKYLYH!