高数基础(一)函数 极限 连续
第一节 函数
导论
函数的概念及常见函数
函数概念

符号函数、取整函数

复合函数

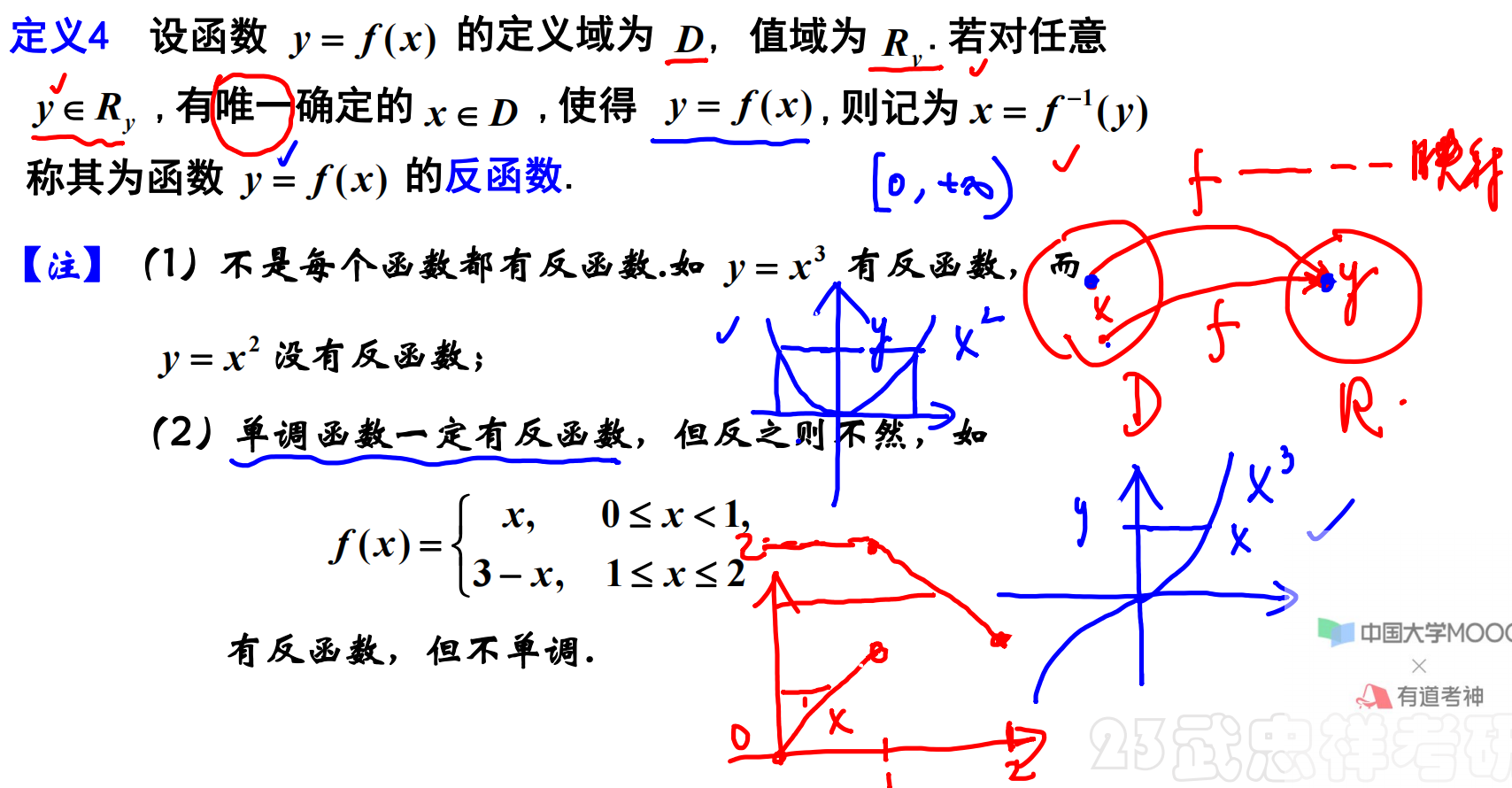
反函数

例题3

初等函数

函数的性质
单调性

奇偶性


例题4
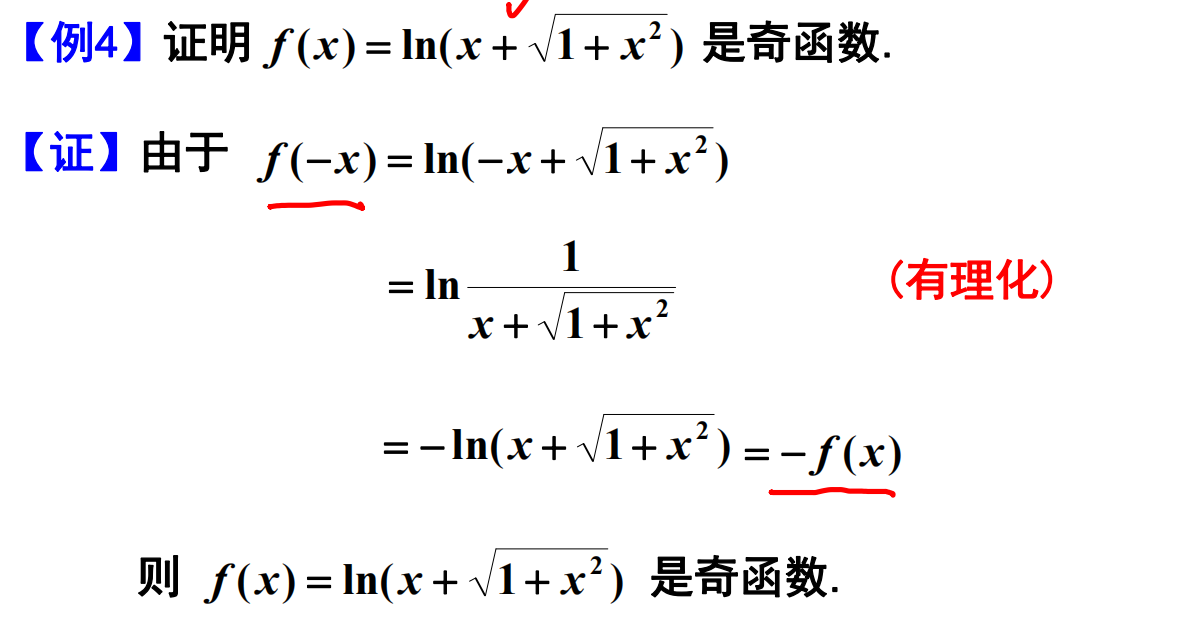
周期性

有界性

例题5

第一节常考题型与典型例题
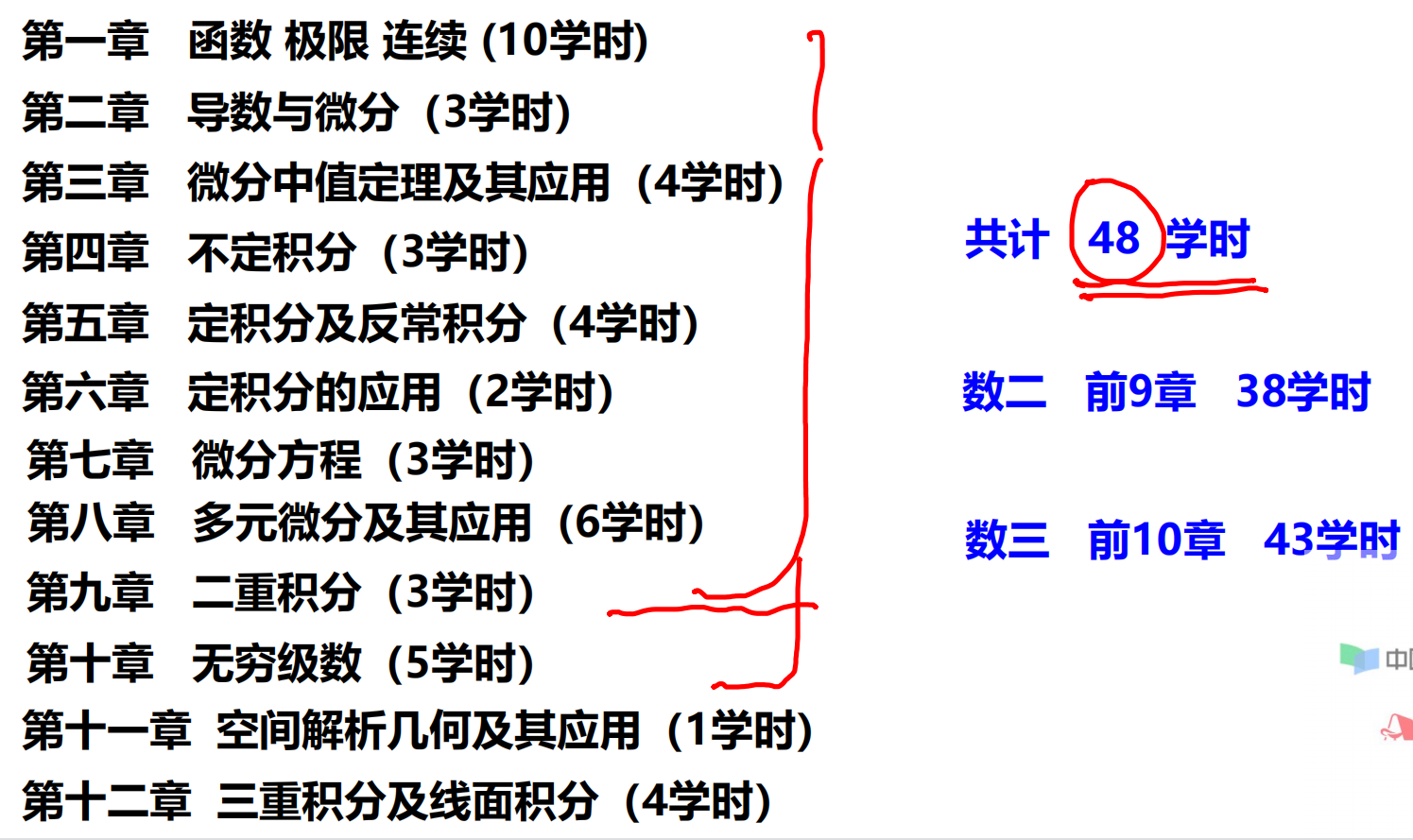
1、函数有界性、单调性、周期性及奇偶性的判定(函数的性质)
2、复合函数
例题6

例题7

例题8

第二节 极限
极限的概念
数列的极限

【注】极限的几何意义:①b<a(a就是极限A),当存在N,当n>N时,x_n>b;②c>a(a就是极限A),当存在N,当n>N时,x_n<c
例题1

例题2

【注】 ||a|-|b||≤|a-b|
函数的极限
自变量趋于无穷大时函数的极限

【注】 函数的极限中x一>∞是指|x|一>+∞(x一>-∞/x一>+∞);而数列极限中的n一>∞是指n一>+∞.
自变量趋于有限值时函数的极限
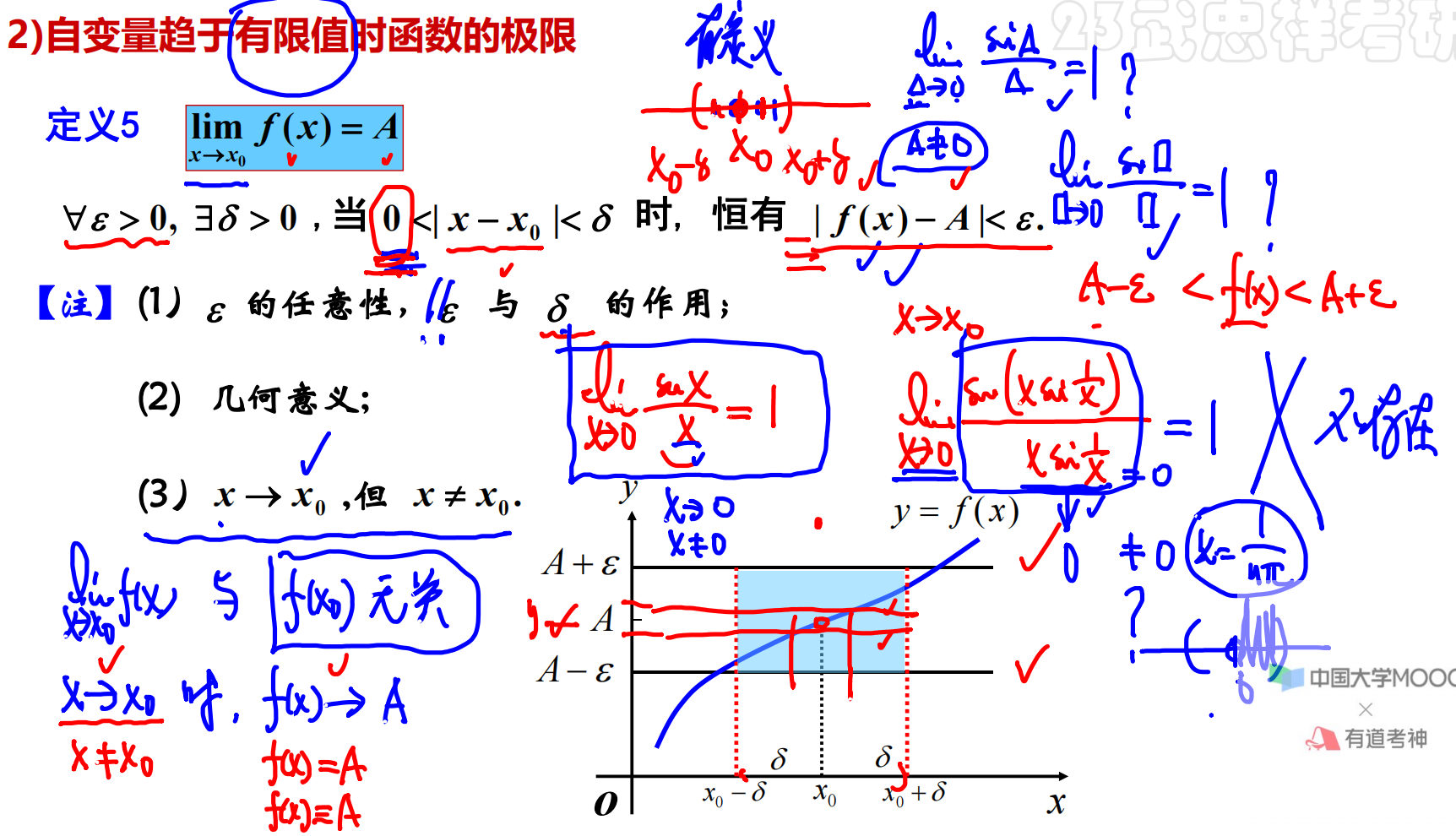


例题3

例题4

极限的性质
有界性

【注】 反之不成立。由此可得有界是数列收敛的必要条件而非充分条件,无界数列一定发散,但发散数列不一定无界。
保号性

例题5


极限值与无穷小之间的关系
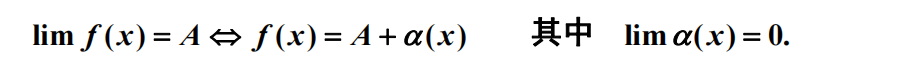
极限的存在准则
夹逼准则
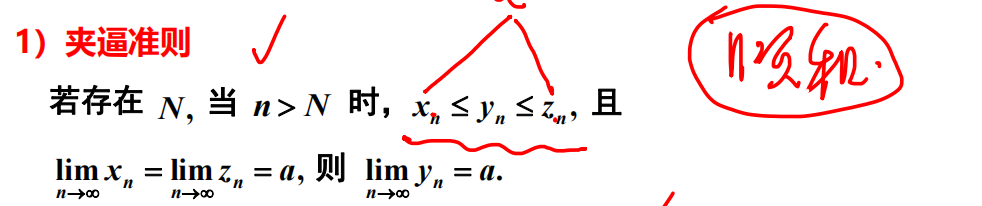
单调有界准则

【注】(1)夹逼准则比较多地用在求n项和的数列极限上,而单调有界准则比较多地是用在求递推关系x_n+1= f(x_n)所定义的数列极限上;(2)函数极限也有对应的以上两条存在准则.
例题6
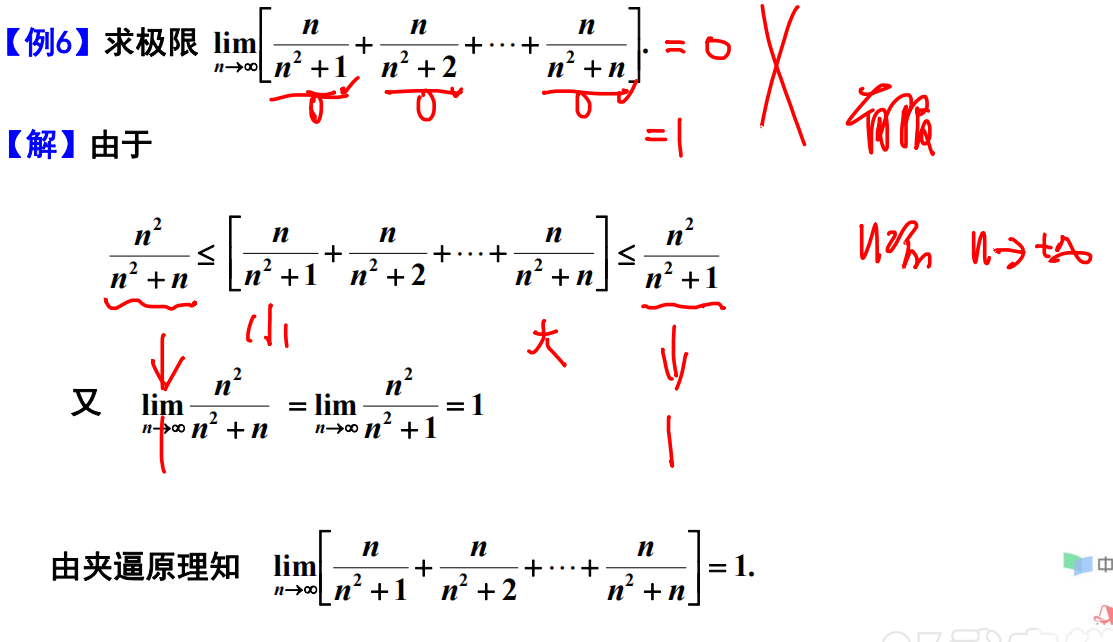
例题7
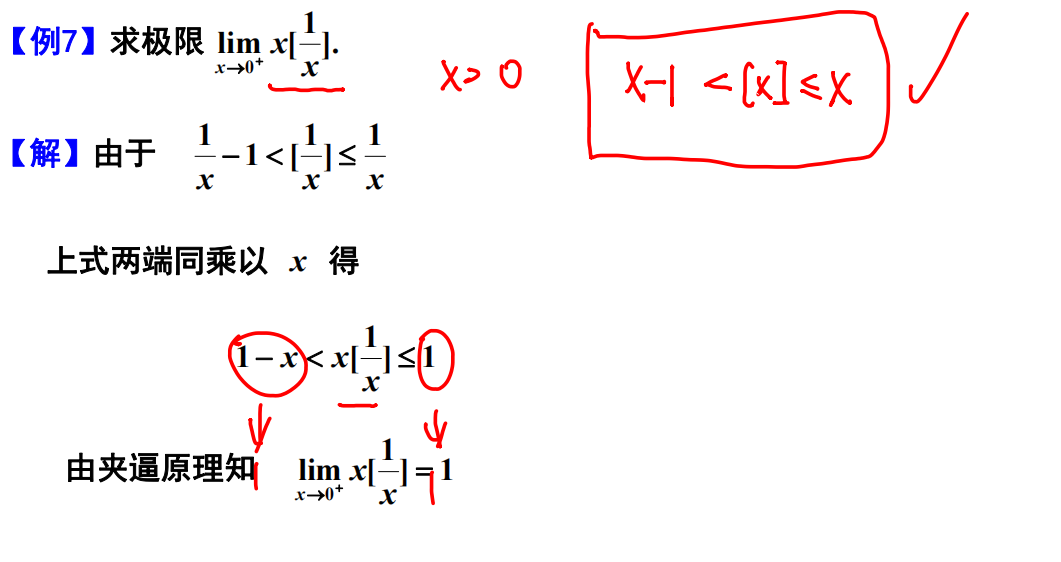
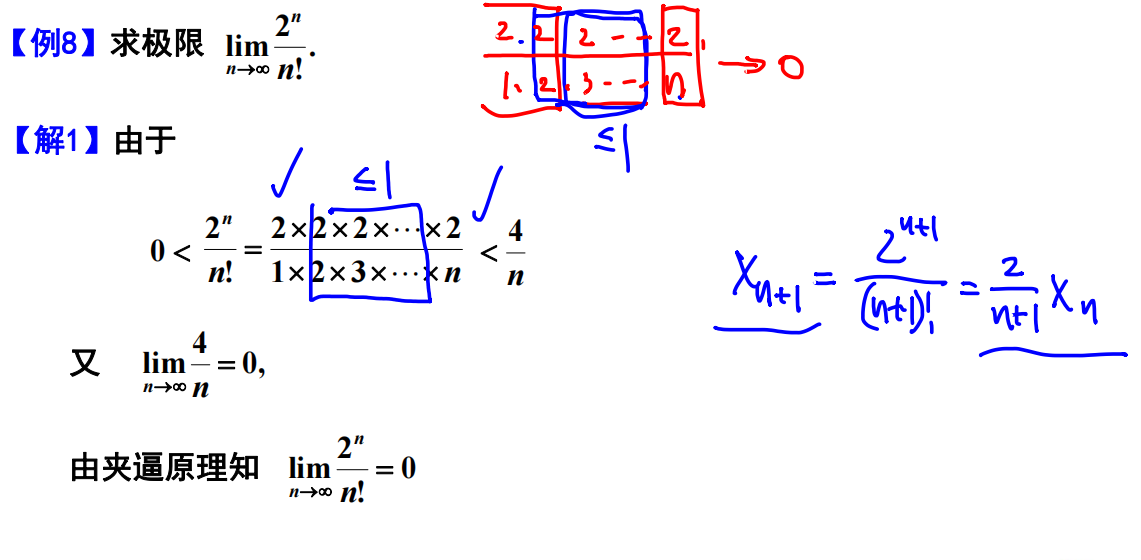
例题8

无穷小量
无穷小量的概念
无穷小量的比较

例题9

无穷小量的性质

无穷大量
无穷大量的概念

常用的一些无穷大量的比较
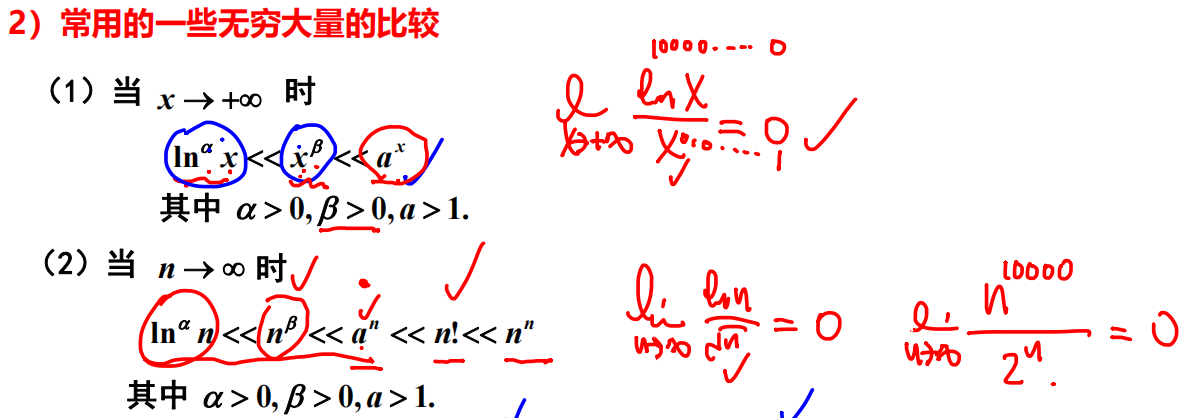
例题10
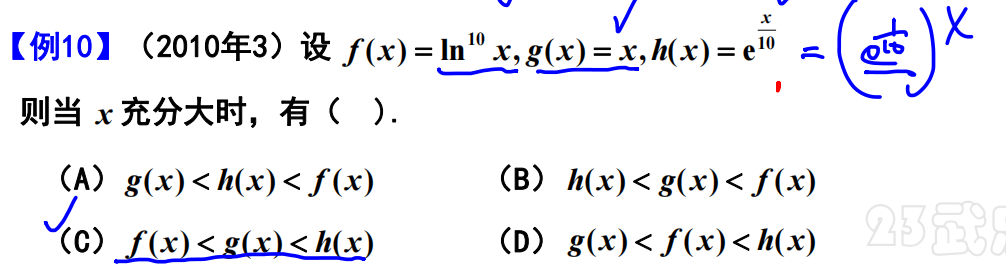
无穷大量的性质

无穷大量与无界变量的关系
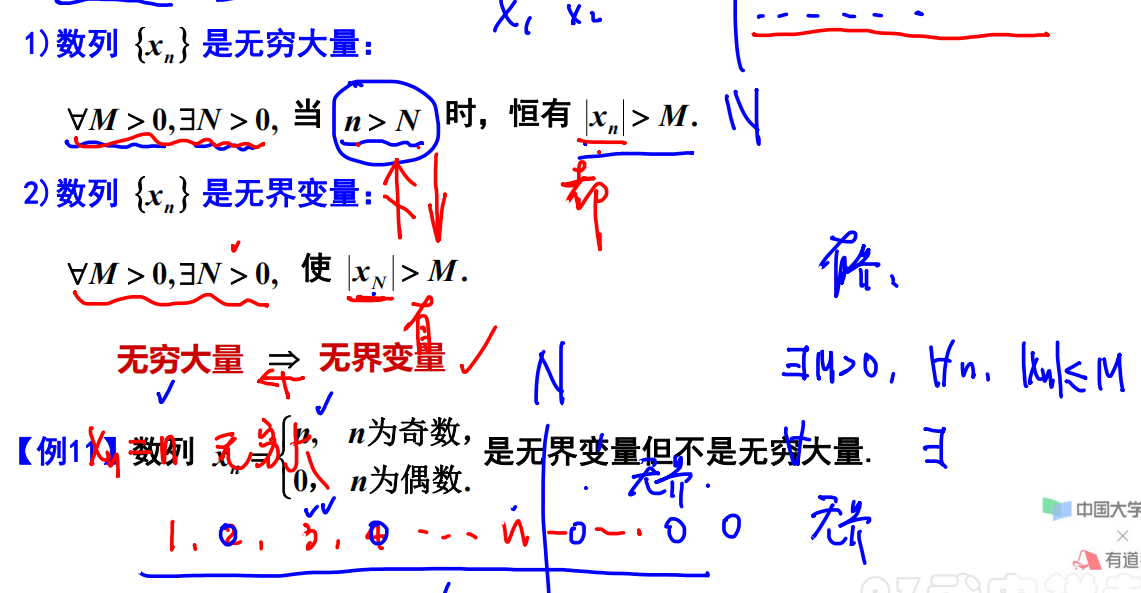
例题12

无穷大量与无穷小量的关系

第二节常考题型与典型例题
1、极限的概念、性质及存在准则
2、求极限(方法:基本极限、等价代换、有理运算)
3、无穷小量阶的比较
极限极限的概念、性质及存在准则
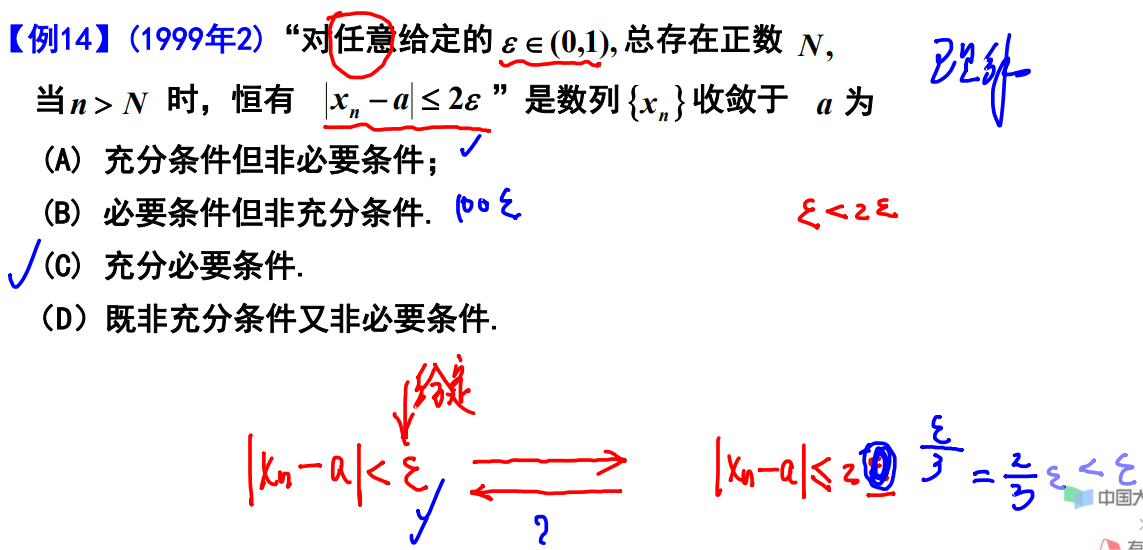
例题14
例题15

例题16

常见的求极限方法(8种)

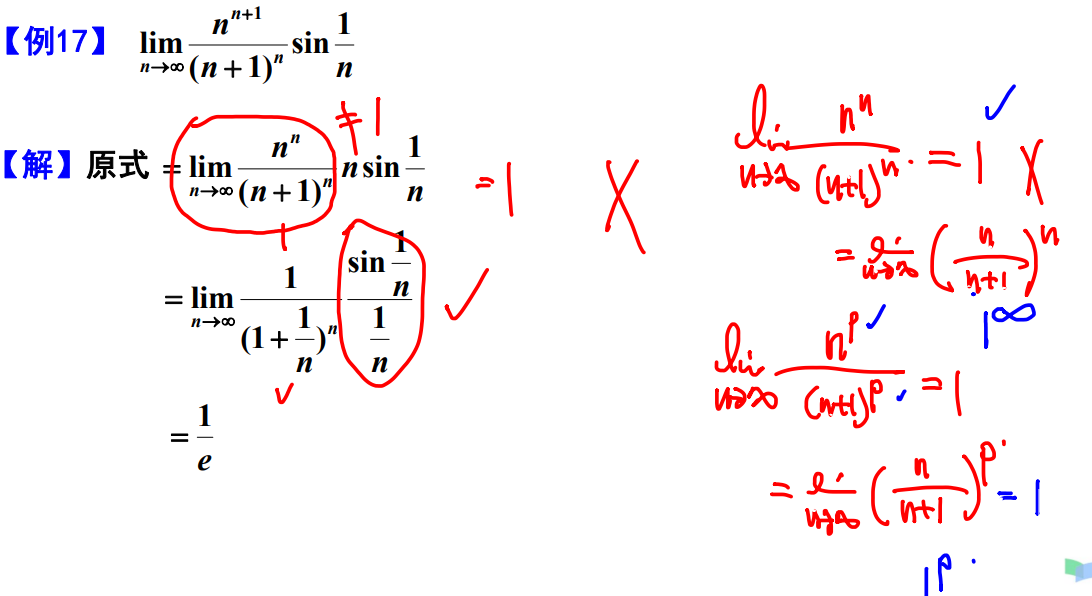
方法1 利用基本极限求极限


例题17
例题18
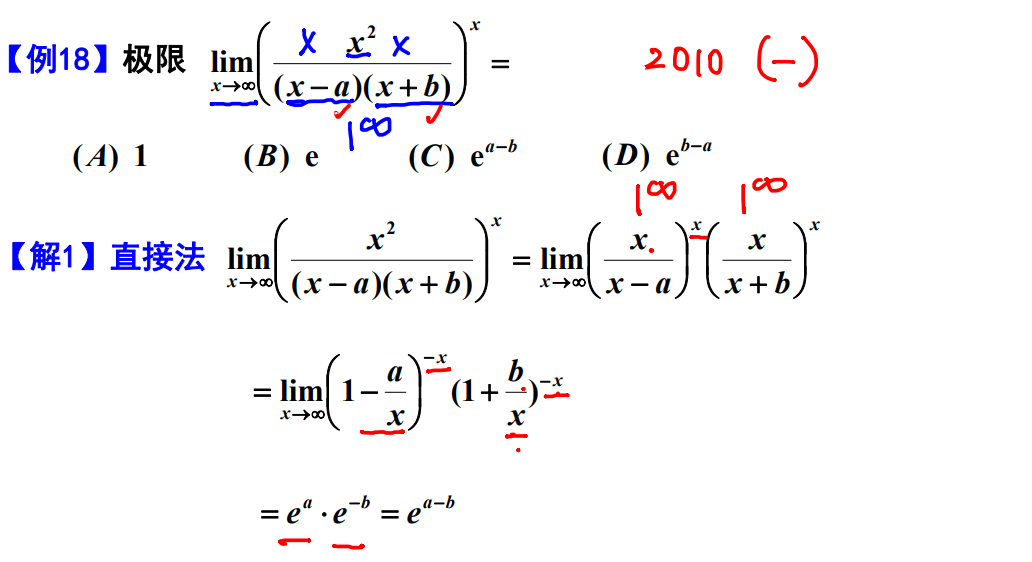
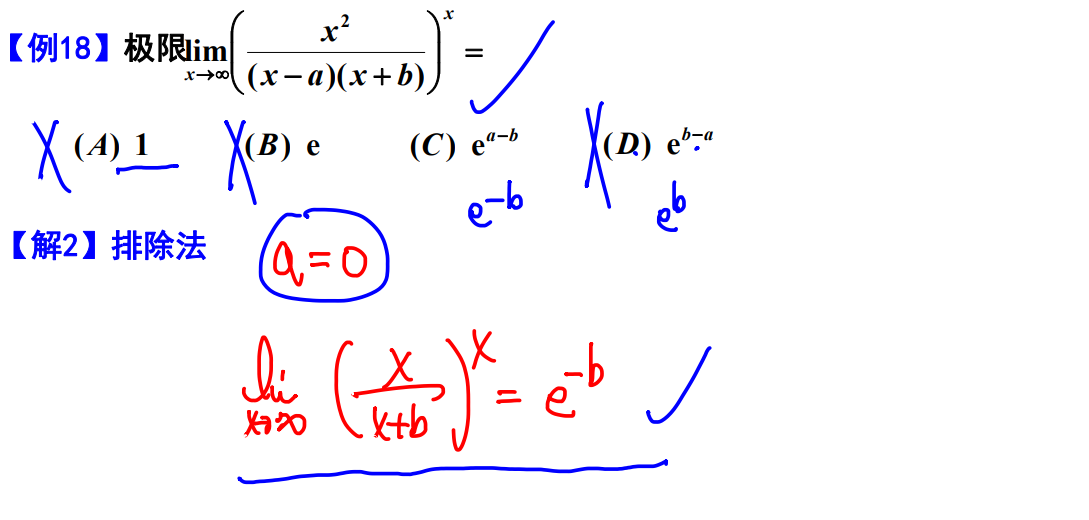
例题19

方法2 利用等价无穷小代换求极限


例题20

例题21

例题22
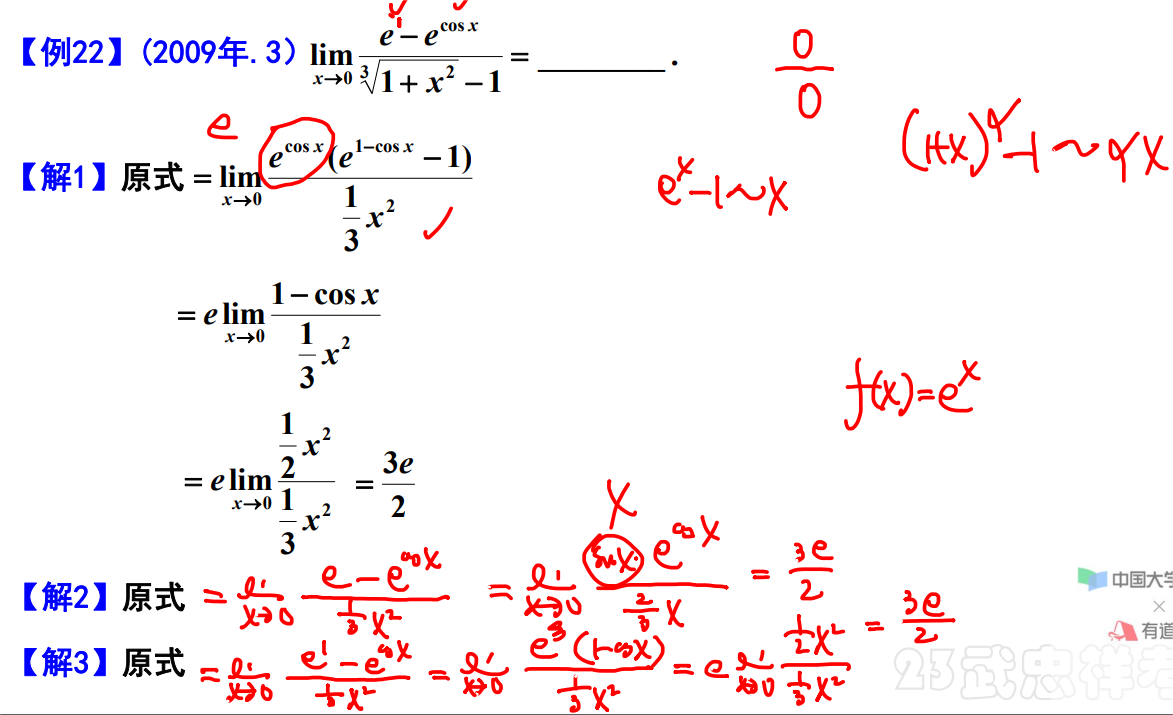
例题23


例题24

例题25

方法3 利用有理运算法则求极限


例题26
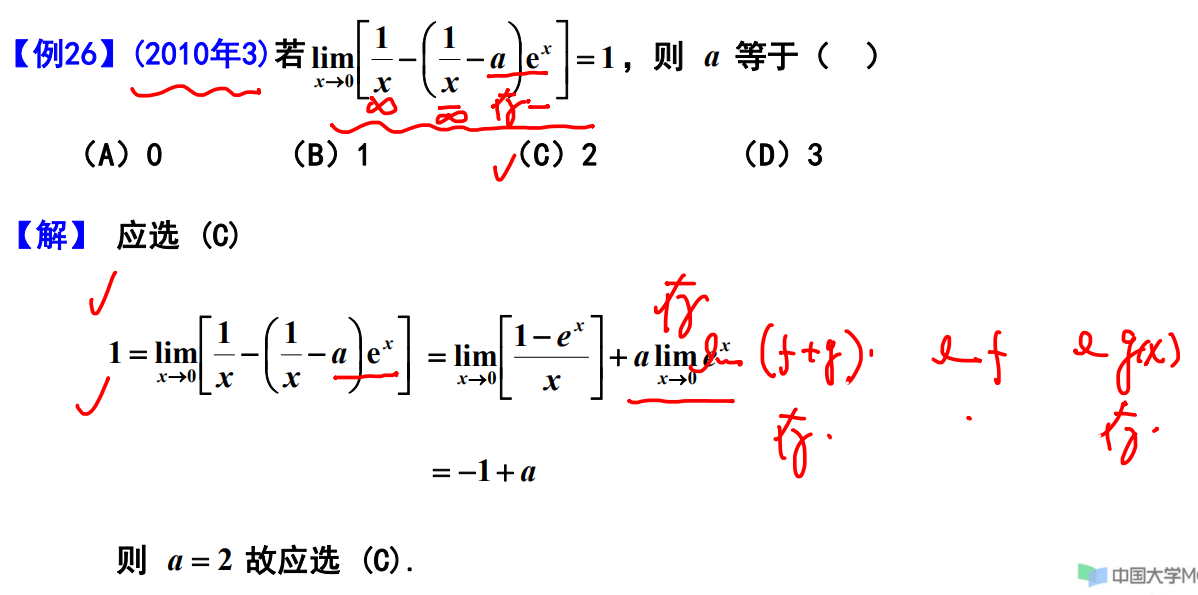
例题27

【注】 lim f(x)g(x) 存在,又f(x)=∞,=》lim g(x)=0
例题28

例题29
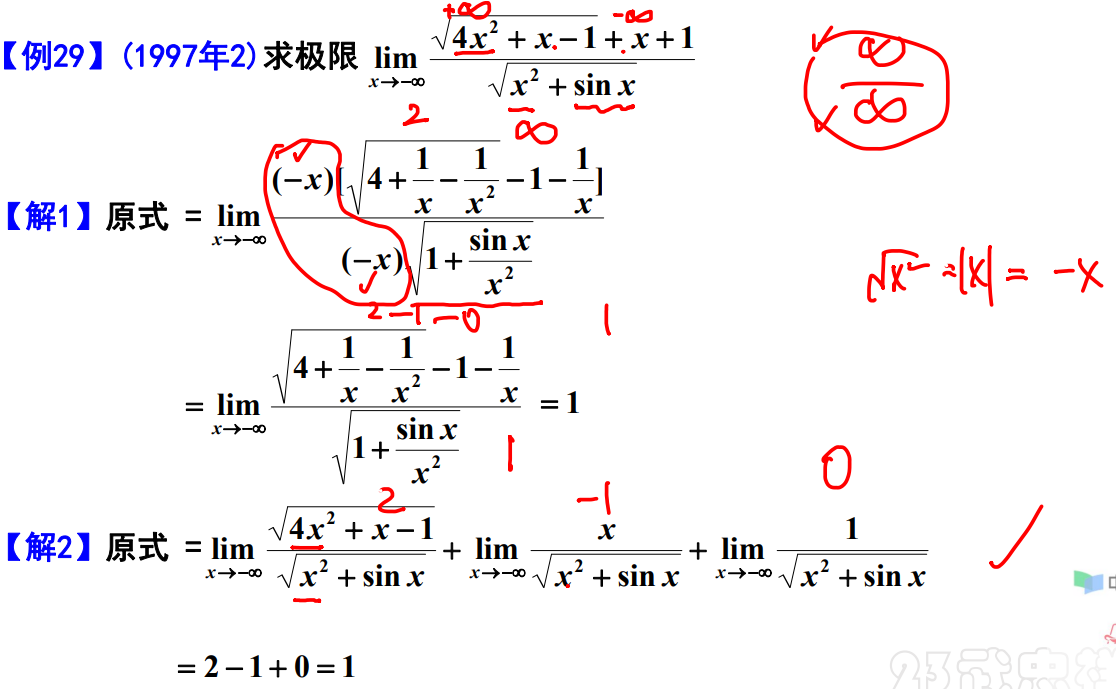
【注】 ∞/∞ =》 (1+n/x)^x=e 或者 (1+n/x)=1
方法4 利用洛必达法则求极限

例题30

例题31

【注】 非零常数因子,先计算出来,放在一起
例题32

例题33


方法5 利用泰勒公式求极限

【注】 ①f(x)=f(0)+f’(0)x+f’’(0)/2!+…+[f^(n)(0)/n!]x^n+o(x^n) ②sin x = x-x^3/3!+…+o(x^2n-1)
例题34

例题35

例题36

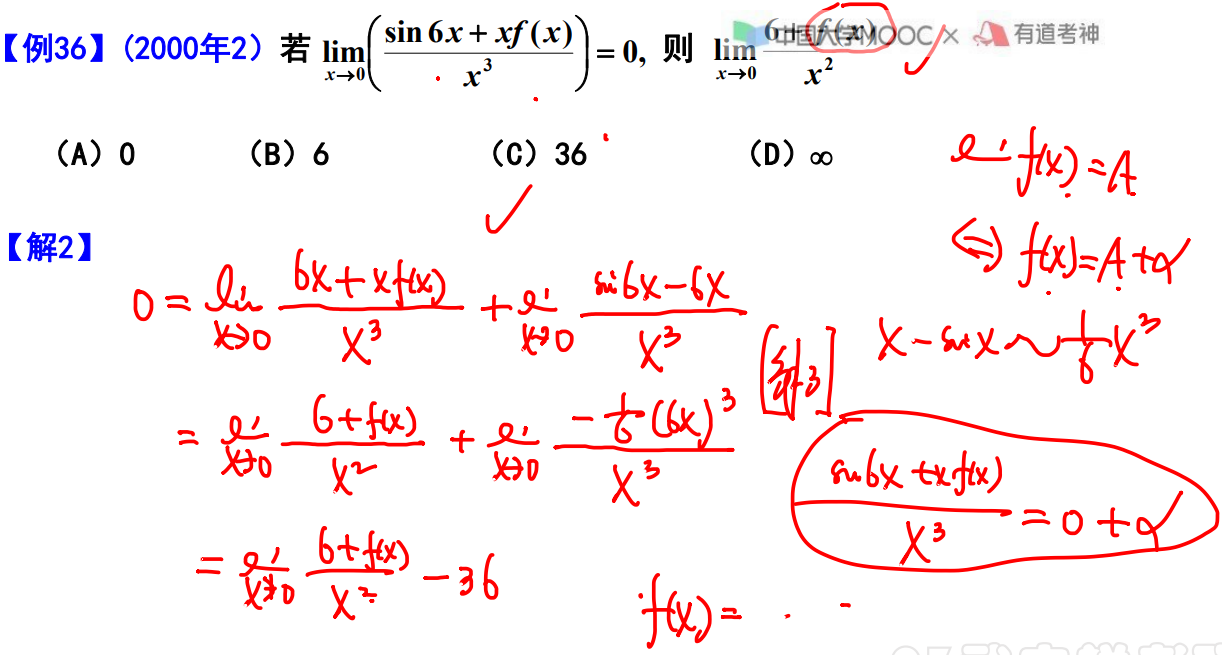
方法6 利用夹逼原理求极限
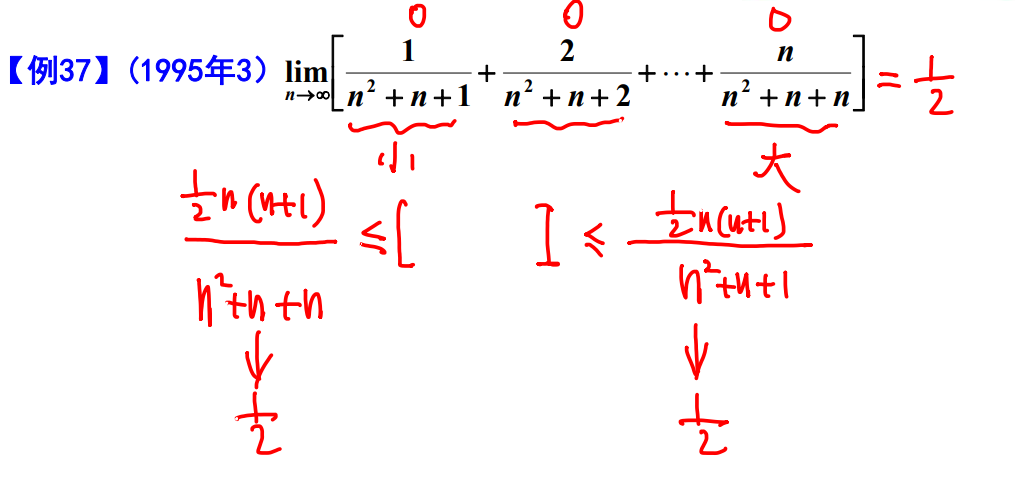
例题38

例题39

【注】 这是一个常用结论
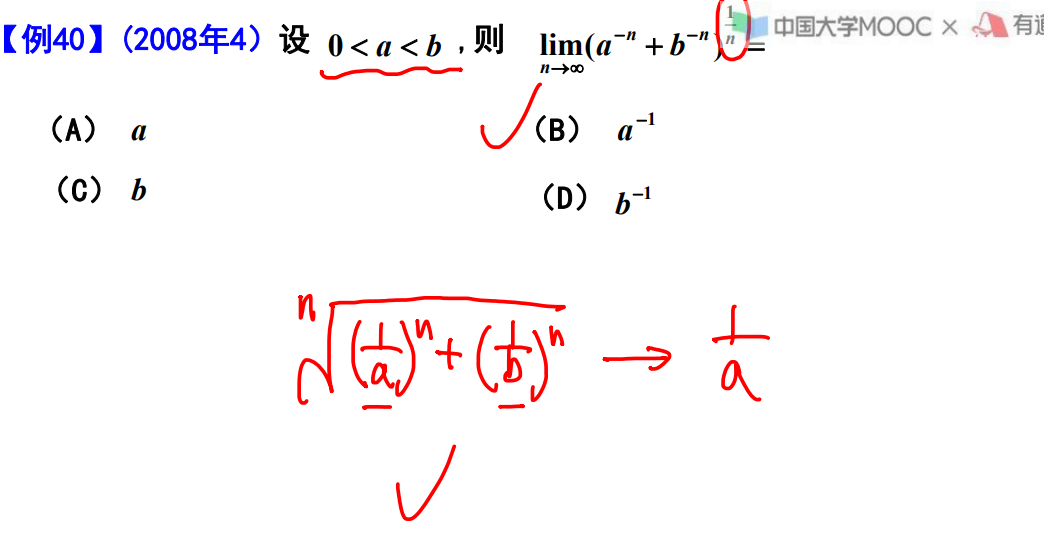
例题40
例题41
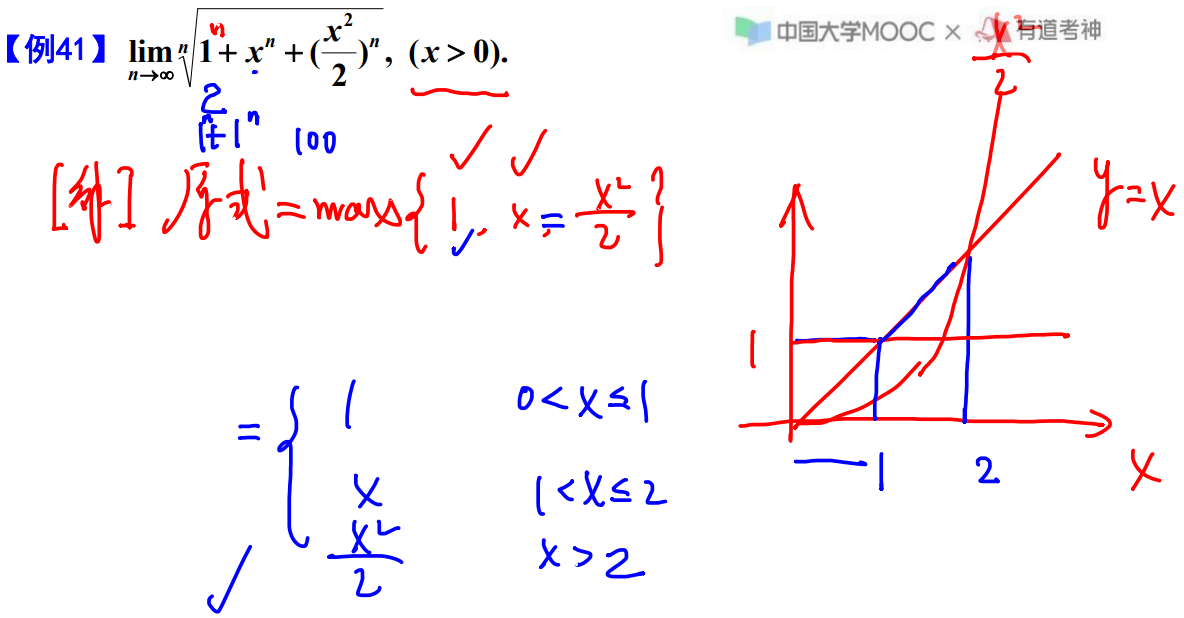
【注】 结论+几何方法
方法7 利用单调有界准则求极限

【注】 ①思路:a. 证存在(单调有界) b. a=f(a) ② 2ab≤a^2+b^2;
方法8 利用定积分定义求极限(见第五章)


【注】 利用定积分定义求极限的一般方法就是先提可爱因子1/n,然后再确定被积函数和积分区间
无穷小量阶的比较
例题43


例题44

例题45

例题46

例题47

第三节 函数的连续性
连续性的概念

例题1

例题2

例题3

间断点及其分类
间断点的定义

间断点的分类

例题4

例题5

连续性的运算与性质

【注】 所谓定义区间,是指包含在定义域内的区间
闭区间上连续函数的性质

【注】 零点定理的一个重要应用就是证明方程的根的存在性
第三节常考题型与典型例题
1、讨论函数的连续性及间断点的类型
2、有关闭区间上连续函数性质的证明题
例题6
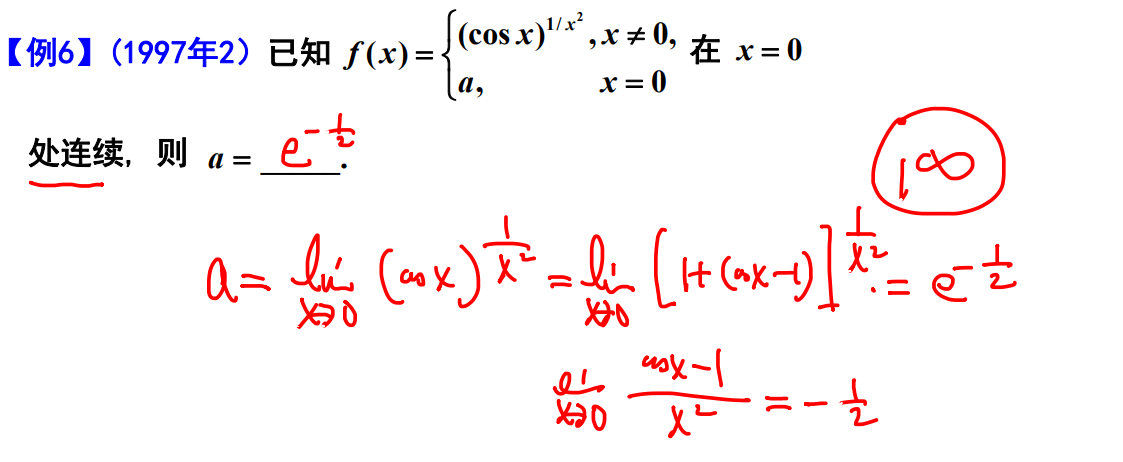
例题7

例题8


例题9
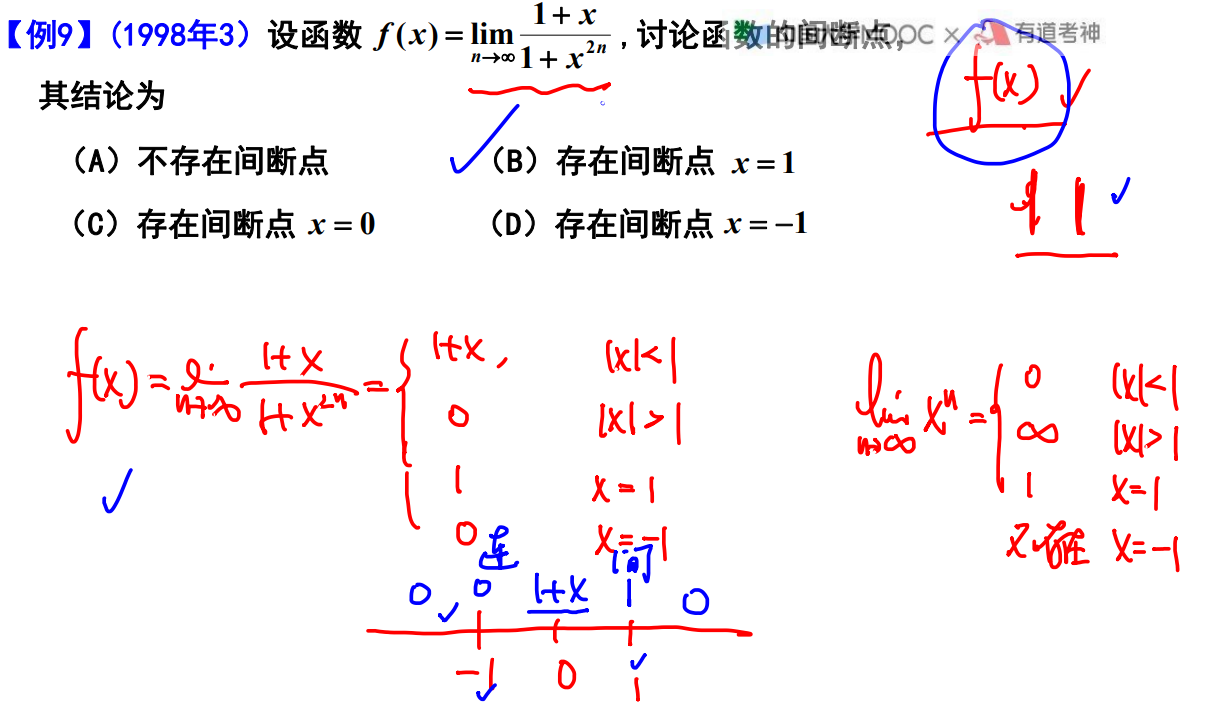
例题10

总结

内容取自武忠祥老师基础班教程,参考书《高等数学·基础篇》